List comprehensions in Python
Python offers a convenient way to handle iterative structures (such as lists, set or dictionaries).
It is considered good practice to be able to manipulate them fluently. Let’s have a look why!
You can get the original notebook here.
Head-first into the topic!
In Python 3, the range keyword does not provide a list but a different structure that can easily be transformed into a list.
range(10)
range(0, 10)
type(range(10)) # this is not a list!
range
list(range(10)) # but you can make a list out of it
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
The key point about this notation is performance: when you write range(10000), you do not create a list of size 10000, but a structure that will give you a new integer each time you go through a loop.
In that perspective, you may be comfortable with the following snippet of code:
for i in range(10):
print (i, end=" ")
0 1 2 3 4 5 6 7 8 9
Now, let’s say we want to compute $x \mapsto 2\cdot x$ for each element of a given list (resp. range).
Let us compare the two following ways of writing it.
a = range(1000000)
%%time
new_list = [2*x for x in a]
CPU times: user 92 ms, sys: 16 ms, total: 108 ms
Wall time: 113 ms
%%time
new_list = []
for x in a:
new_list.append(x)
CPU times: user 172 ms, sys: 36 ms, total: 208 ms
Wall time: 207 ms
Any syntax going like
[f(x) for x in array] is referred to as list comprehension.
The official docs.python.org mentions it quickly here but let’s go through this more into details.
List comprehensions are not only about lists
List comprehensions are based on a Python specific data structure called a generator.
You can manipulate a generator with brackets (no bracket results in a SyntaxError).
g = (str(i) for i in range(10))
type(g)
generator
You can construct any data structure that accept iterable structures with a generator.
list(g)
['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
Note that the generator is now empty. You cannot build a second list from the same g:
list(g)
[]
So let’s go through different constructions:
- the regular Python
list:
# equivalent notations for lists
list(str(i) for i in range(10))
[str(i) for i in range(10)]
['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
- the regular Python
set:
# equivalent notations for sets
set(str(i) for i in range(10))
{str(i) for i in range(10)}
{'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'}
- even dictionaries (keyword
dict) with the column character:
{i: str(i) for i in range(10)}
{0: '0',
1: '1',
2: '2',
3: '3',
4: '4',
5: '5',
6: '6',
7: '7',
8: '8',
9: '9'}
There are actually other useful constructions, e.g. sorted that builds a sorted list from a generator:
[i*(-1)**(i) for i in range(10)]
[0, -1, 2, -3, 4, -5, 6, -7, 8, -9]
sorted(i*(-1)**(i) for i in range(10))
[-9, -7, -5, -3, -1, 0, 2, 4, 6, 8]
Building a set from the generator can also be useful as reflected on the following snippet:
[i**2 for i in range(-5, 5)]
[25, 16, 9, 4, 1, 0, 1, 4, 9, 16]
{i**2 for i in range(-5, 5)}
{0, 1, 4, 9, 16, 25}
You can also build there structures with more complex constructions.
Recall the enumerate and/or zip constructions:
french = ["un", "deux", "trois", "cat", "sank"]
english = ["one", "two", "three", "four", "five"]
words = { i+1: f for i, f in enumerate(zip(french, english)) }
words
{1: ('un', 'one'),
2: ('deux', 'two'),
3: ('trois', 'three'),
4: ('cat', 'four'),
5: ('sank', 'five')}
Looping on a dictionary iterates on the keys:
[str(s) for s in words]
['1', '2', '3', '4', '5']
But you can also use the dict.items() method.
Here is an example to show there is “no” limit in how you can use list comprehensions.
[[key, value[0], len(value[0]), value[1].upper(), len(value[1])]
for key, value in words.items()]
[[1, 'un', 2, 'ONE', 3],
[2, 'deux', 4, 'TWO', 3],
[3, 'trois', 5, 'THREE', 5],
[4, 'cat', 3, 'FOUR', 4],
[5, 'sank', 4, 'FIVE', 4]]
Common loop patterns using list comprehensions
Check the difference between a zip and a double loop construction:
list(zip(french, english))
[('un', 'one'),
('deux', 'two'),
('trois', 'three'),
('cat', 'four'),
('sank', 'five')]
[(x, y) for x in french for y in english]
[('un', 'one'),
('un', 'two'),
('un', 'three'),
('un', 'four'),
('un', 'five'),
('deux', 'one'),
('deux', 'two'),
('deux', 'three'),
('deux', 'four'),
('deux', 'five'),
('trois', 'one'),
('trois', 'two'),
('trois', 'three'),
('trois', 'four'),
('trois', 'five'),
('cat', 'one'),
('cat', 'two'),
('cat', 'three'),
('cat', 'four'),
('cat', 'five'),
('sank', 'one'),
('sank', 'two'),
('sank', 'three'),
('sank', 'four'),
('sank', 'five')]
You can also add conditions withing the list comprehension:
[a for a in range(10) if a % 2 == 0]
[0, 2, 4, 6, 8]
(a, b, c) integers such that $$a^2 + b^2 = c^2$$
[ (a, b, c) for a in range(1, 30)
for b in range(a, 30)
for c in range(b, 30) if a**2 + b**2 == c**2 ]
[(3, 4, 5),
(5, 12, 13),
(6, 8, 10),
(7, 24, 25),
(8, 15, 17),
(9, 12, 15),
(10, 24, 26),
(12, 16, 20),
(15, 20, 25),
(20, 21, 29)]
Note that you can also use nested list comprehensions.
[[(x, y) for x in french] for y in english]
[[('un', 'one'),
('deux', 'one'),
('trois', 'one'),
('cat', 'one'),
('sank', 'one')],
[('un', 'two'),
('deux', 'two'),
('trois', 'two'),
('cat', 'two'),
('sank', 'two')],
[('un', 'three'),
('deux', 'three'),
('trois', 'three'),
('cat', 'three'),
('sank', 'three')],
[('un', 'four'),
('deux', 'four'),
('trois', 'four'),
('cat', 'four'),
('sank', 'four')],
[('un', 'five'),
('deux', 'five'),
('trois', 'five'),
('cat', 'five'),
('sank', 'five')]]
Similar functions in numpy
Python loops are known to be expensive. List comprehensions help, but numpy takes a different approach by unfolding the loops using code written in C.
import numpy as np
%%time
new_list = [2*x for x in range(1000000)]
CPU times: user 84 ms, sys: 32 ms, total: 116 ms
Wall time: 119 ms
a = np.arange(1000000)
%%time
new_list = 2 * a
CPU times: user 20 ms, sys: 0 ns, total: 20 ms
Wall time: 21.9 ms
- Nested comprehension may remind you the
meshgridfunction:
z = [[ (x+y) for x in range(10)] for y in range(5)]
z
[[0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
[4, 5, 6, 7, 8, 9, 10, 11, 12, 13]]
a, b = np.meshgrid(np.arange(10), np.arange(5))
c = a + b
c
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 2, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[ 3, 4, 5, 6, 7, 8, 9, 10, 11, 12],
[ 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]])
- You can go through elements of a 2D array with the following constructs:
[col[1] for col in z]
[1, 2, 3, 4, 5]
c[:, 1]
array([1, 2, 3, 4, 5])
Be careful though that numpy does not provide you a fresh copy of the array even if you create intermediate references.
d = c[:, 0]
d *= 0
c
array([[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9],
[ 0, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[ 0, 3, 4, 5, 6, 7, 8, 9, 10, 11],
[ 0, 4, 5, 6, 7, 8, 9, 10, 11, 12],
[ 0, 5, 6, 7, 8, 9, 10, 11, 12, 13]])
Yet another implementation for this old academic problem
Say we want to get all the prime numbers lesser than n.
List comprehension can be a comfortable way to compute the sieve of Eratosthenes.
%%timeit
# First compute the non prime numbers
nope = [j for i in range(2, 8) for j in range(i*2, 50, i)]
# Then build a new list not containing prime numbers
[x for x in range(2, 50) if x not in nope]
10000 loops, best of 3: 33.9 µs per loop
Actually the following implementation with sets may be more space and time efficient:
%%timeit
sieve = set(range(2, 50))
for i in range(2, 8):
sieve -= set(range(2*i, 50, i))
sieve
100000 loops, best of 3: 9.82 µs per loop
Another way to build your own generators
Let’s recall the types of the structures we mentioned:
type(range(10))
range
type(i for i in range(10))
generator
Python provides a yield keyword in order to let you write your own generator objects.
When the program hits a yield keyword:
- it yields the current value,
- then waits for the next iteration in a loop (see the
__next__keyword), - then re-enters the program where it was last interrupted.
The Syracuse suite is a good study case for this programming style.
See in the doctest how we build the suite using the list constructor on a generator structure.
def syracuse(n):
"""Computes the Syracuse suite.
>>> list(p for p in syracuse(28))
[28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1]
"""
assert n > 0
yield n
while n != 1:
if n & 1 == 0:
n = n // 2
else:
n = 3 * n + 1
yield n
An interesting plot to draw is the length of the Syracuse list for all integers within a certain range. See how confortable it can be to write it.
%matplotlib inline
import matplotlib.pyplot as plt
def length(iterable):
"""Length of a generator.
The `len` keyword does not apply on generators.
This makes the trick without expanding the list!
"""
return sum(1 for _ in iterable)
# Note how we can pass a range to `plt.plot`, not necessarily a list
# Note the multi-level generator in the second part of the array
interval = range(1, 1000)
plt.plot(interval, [length(syracuse(i)) for i in interval], "r.")
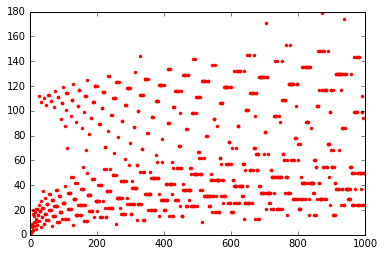
[i for i in range(1, 50) if length(syracuse(i)) > 100]
[27, 31, 41, 47]
27 is the first integer when the Syracuse suite length exceeds 100.
We can pretty-print the suite with another kind of list comprehension.
print(" ⇢ ".join(str(i) for i in syracuse(27)))
27 ⇢ 82 ⇢ 41 ⇢ 124 ⇢ 62 ⇢ 31 ⇢ 94 ⇢ 47 ⇢ 142 ⇢ 71 ⇢ 214 ⇢ 107 ⇢ 322 ⇢ 161 ⇢
484 ⇢ 242 ⇢ 121 ⇢ 364 ⇢ 182 ⇢ 91 ⇢ 274 ⇢ 137 ⇢ 412 ⇢ 206 ⇢ 103 ⇢ 310 ⇢ 155 ⇢
466 ⇢ 233 ⇢ 700 ⇢ 350 ⇢ 175 ⇢ 526 ⇢ 263 ⇢ 790 ⇢ 395 ⇢ 1186 ⇢ 593 ⇢ 1780 ⇢
890 ⇢ 445 ⇢ 1336 ⇢ 668 ⇢ 334 ⇢ 167 ⇢ 502 ⇢ 251 ⇢ 754 ⇢ 377 ⇢ 1132 ⇢ 566 ⇢
283 ⇢ 850 ⇢ 425 ⇢ 1276 ⇢ 638 ⇢ 319 ⇢ 958 ⇢ 479 ⇢ 1438 ⇢ 719 ⇢ 2158 ⇢ 1079 ⇢
3238 ⇢ 1619 ⇢ 4858 ⇢ 2429 ⇢ 7288 ⇢ 3644 ⇢ 1822 ⇢ 911 ⇢ 2734 ⇢ 1367 ⇢ 4102 ⇢
2051 ⇢ 6154 ⇢ 3077 ⇢ 9232 ⇢ 4616 ⇢ 2308 ⇢ 1154 ⇢ 577 ⇢ 1732 ⇢ 866 ⇢ 433 ⇢
1300 ⇢ 650 ⇢ 325 ⇢ 976 ⇢ 488 ⇢ 244 ⇢ 122 ⇢ 61 ⇢ 184 ⇢ 92 ⇢ 46 ⇢ 23 ⇢ 70 ⇢
35 ⇢ 106 ⇢ 53 ⇢ 160 ⇢ 80 ⇢ 40 ⇢ 20 ⇢ 10 ⇢ 5 ⇢ 16 ⇢ 8 ⇢ 4 ⇢ 2 ⇢ 1
plt.plot(list(syracuse(27)))
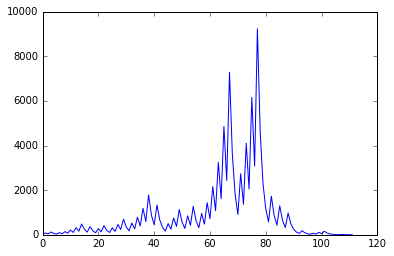
We can see the suite goes up to 9232 (!) before coming back (quite fast) down to [4, 2, 1].
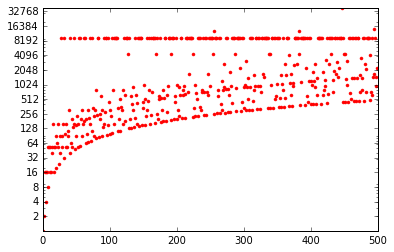
Another interesting plot shows the height of the suite for each integer.
max is also a construction that accepts a generator as parameter!
ax = plt.gca()
ax.set_yscale('log')
ax.set_yticks([1 << i for i in range(1, 17)])
ax.set_yticklabels([1 << i for i in range(1, 17)])
interval = range(1, 500)
plt.plot(interval, [max(syracuse(i)) for i in interval], "r.")
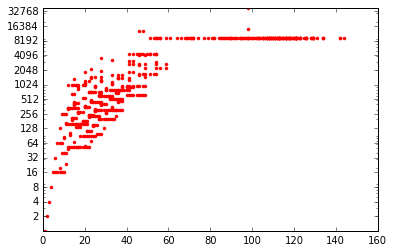
A last interesting graph plots the height of a suite depending on its length.
ax = plt.gca()
ax.set_yscale('log')
ax.set_yticks([1 << i for i in range(1, 17)])
ax.set_yticklabels([1 << i for i in range(1, 17)])
interval = range(1, 500)
plt.plot([length(syracuse(i)) for i in interval],
[max(syracuse(i)) for i in interval], "r.")
Read more about it
Make sure to have a look at the following links:
- The PEP about list comprehensions;
- An interesting story about code optimisation;
- More about this new notation


