Constraint programming

« Previous | Up ↑ | Next »

Definition

A constraint satisfaction problem consists of:

• a finite set of variables $x_1,… x_n$;
• a corresponding set of finite domains $d_1, … d_n$;
• a finite set of constraints over subsets of variables, i.e. relations expressing which assignations of variables to values are acceptable.

The objective is to find an instantiation of values to variables within their domains, which satisfies all the expressed constraints.

A problem of two variables $x, y \in {0, 1, 2}$ subject to the constraint $x \neq y$ is a constraint satisfaction problem.

• Unlike Linear Programming, there is no restriction on the nature of constraints as long as the solver is able to determine for any instantiation if it violates any of the constraints stated.^[If you can explain the constraint with words in proper English, you can probably state it using constraint programming.]
• It is not possible to manipulate infinite domains.
• In theory, the domains can be formed of anything. However, it is a common practice to associate these pieces of anything with finite sets of integers.

Illustrative problems

\[\begin{alignat*}{12} &&&&&&\sf{}S&&\sf{}E&&\sf{}N&&\sf{}D\\ &&+&&&&\sf{}M&&\sf{}O&&\sf{}R&&\sf{}E\\ =&&&&\sf{}M&&\sf{}O&&\sf{}N&&\sf{}E&&\sf{}Y \end{alignat*}\]

Exercice:
Which digits can we use to replace the following letters so that the addition stands true?

Solution (Click to unfold)

Each letter can be associated to a variable taking values between 0 and 9. All variables are linked by the following arithmetic constraint $\mathsf S \times 1000 + \mathsf E \times 100 + ... = ... + \mathsf E \times 10 + \mathsf Y$.

Exercice:
Place 8 queens on a board so that no two queens attack each other.

Solution (Click to unfold)

Eight variables $q_i$ represent the position of the queen placed on the row labeled $i$. All variables must be different (not on the same column). Also, no two queens may be placed on the same ($\nearrow$ and $\searrow$) diagonal.

Exercice:
How to colour each region of the attached map, so that no two neighbouring regions hold the same colour? The problem consists in finding a colouring that minimises the number of colours used to paint the map.

Solution (Click to unfold)

Each region is mapped to a colour (integer) taking values between 1 and n. A different ($\neq$) constraint is stated over all regions that are neighbouring.

You may recall the mathematical theorem stating that at most four colours are necessary for a proper colouring of such maps. We can use $n=4$ for a start (upper bound) and choose to decrease $n$ until no solution is found.

A more complicated—albeit general—approach would be to add an minimising criterion (optimisation) on the total number of colours used in a satisfying colouring.

The resolution process

Constraints as we state them do not necessarily apply to all variables which we use to define the problem.
Each constraint is associated with:

• its scope, i.e. the set of variables it applies on;
• its arity, i.e. the number of variables it applies on.

A common resolution process implements a depth-first search algorithm in a tree that is built on the fly:

• We first choose an ordering over the variables: $x_1, x_2, \cdots x_n$;
• The first branch of the first level of the tree maps to the instantiation of the first possible value of variable $x_1$. From this node, the first branch (of the second level) of the tree maps appends to the preceding partial instantiation the instantiation of the first possible value for variable $x_2$;
• The algorithm stops when it reaches a leaf (a.k.a. full instantiation) which violates no constraint.
• At each node (a.k.a. partial instantiation), the algorithm checks the validity of all constraints whose scope is included in the set of already assigned variables:
  • if no conflict is raised, the search goes deeper and a new variable is assigned;
  • if a conflict is raised, the search goes backward and invalidates the assumptions already made.

• The choice of the variable and/or value order can have a significant impact on the size of the tree, i.e. on the resolution time. Some heuristics (e.g., choose first the variable with the smaller domain) may yield better performance.
• Do keep in mind that no tree is actually built in memory: the branching is made on the fly and the tree representation only illustrates the algorithm.

A word about arc-consistency

In the worst case, the tree is of an exponential size: efficient algorithms try to prune sub-trees as early as possible in the depth-first search process.

The basic backtracking algorithm we implemented on the toy problem shows several issues:

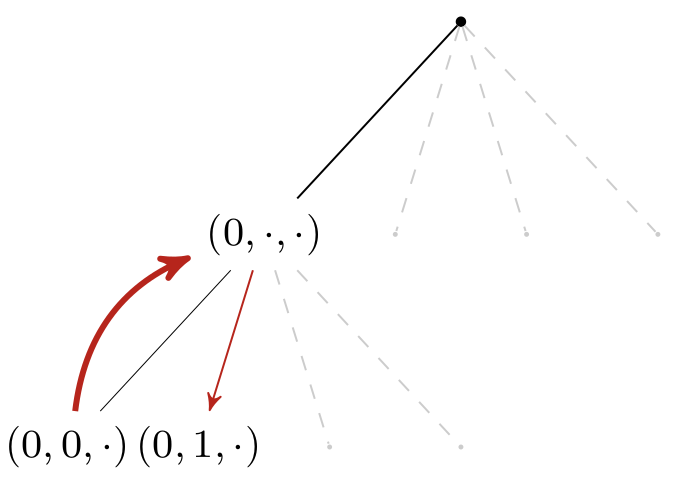
• the domain of $x_3$ should be limited to ${1, 2, 3}$ to avoid countless instantiations of value $0$ to variable $x_3$ and subsequent backtracking.
• a similar domain reduction should be implemented on binary constraints. If $c_1: x_1 \neq x_2$, assigning value $0$ to $x_1$ should remove $0$ from the domain of $x_2$ in the sub-tree rooted in $(0,\cdot,\cdot)$.

Important!
This step is called constraint propagation and is something we as humans are very capable at doing (unlike a search tree). In fine, Constraint programming is all about alternating hypotheses (branching) and constraint propagation (pruning).

A basic implementation of constraint propagation consists of maintaining arc-consistency, i.e. pruning the domains of variables which are not yet assigned but linked to assigned variables through binary constraints.

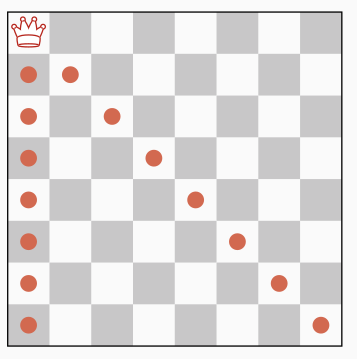
We can illustrate the benefits of this forward-checking approach with the 8-queen problem. When the first (red) queen is placed, we prune the domain of all the other queens (red dots).

Then, instead of trying position 1 and 2, the second (green) queen is directly placed on the first value of its subsequent domain, i.e. position 3.

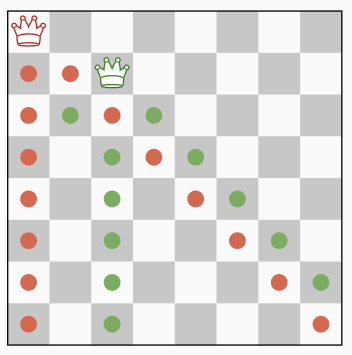
When the third (blue) queen is placed, the domain of the sixth queen is reduced a single value (i.e. position 4);

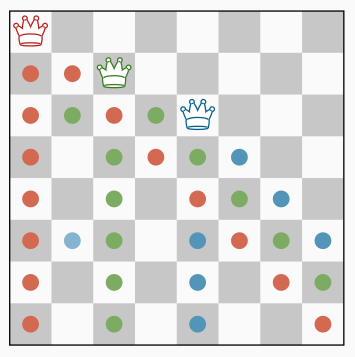
however, the placement of the fourth (violet) queen eliminates all values of the domain of this queen. A backtrack can be triggered at that point.

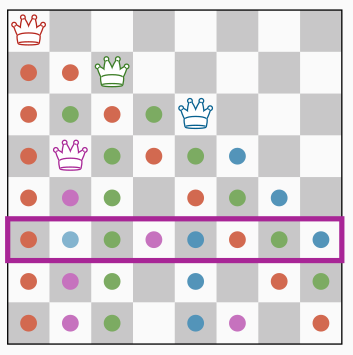
Note that with this arc-consistency technique, the first backtrack occurs for instance $(1,3,5,2,\cdot,\cdot,\cdot,\cdot)$. Without this optimisation, we would have already backtracked 7 times before reaching this partial instantiation, and would still need to make several attempts/backtracks for queens #5 and #6 before realising they lead to no solution.

There are many algorithms designed to maintain arc-consistency and detect irrelevant sub-trees as soon as possible.

Symmetries

Consider the n-queen problem. A chessboard that is rotated by 90°, 180° or 270° yields queens positions that are different yet equivalent.

If the former chessboard is a solution to our problem, the latter also is. Conversely, if the former violates any constraint, the latter does so as well. A mirrored chessboard follows the same logics.

Formally speaking, a symmetry may be a permutation on the variables ($q_1 \rightleftharpoons q_4$) and/or on the values ($1 \rightleftharpoons 4$) of the problem.

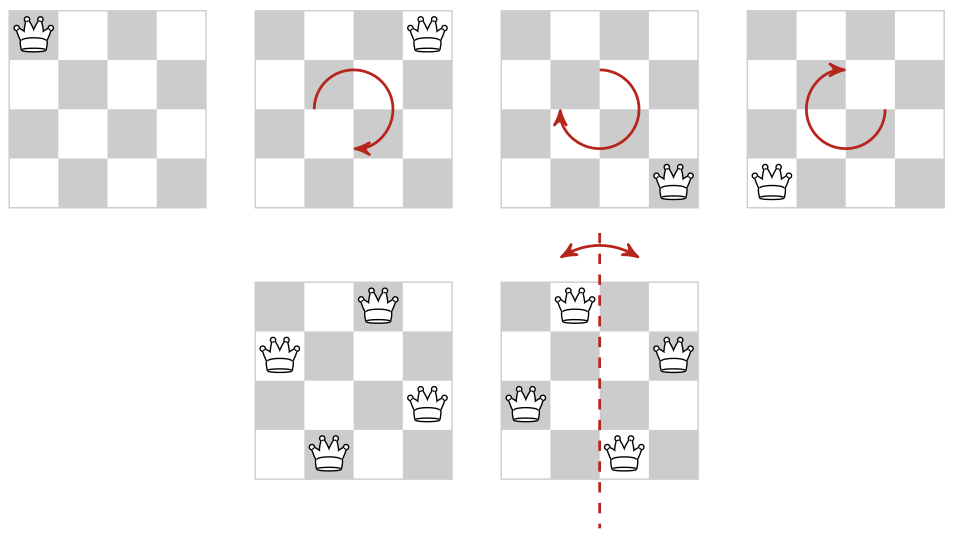
There are several ways to exploit the symmetries of a problem:

• reformulate a problem into a simpler one without symmetries. The tree to be searched is of a smaller size than the symmetrical one, leading to significantly better performance.
  As a matter of fact, it is important to find a good balance when writing models: avoid symmetries yet still be readable.

• add constraints to the problem so as to break the symmetries. The constraints may be added statically (before the search) or dynamically (during the search by the solver).
  Tip: when several variables $x_i$ can be swapped in a problem, consider constraining them with an ordering: $x_1 \leq x_2 \leq \cdots x_n$.

• the solver may dynamically use symmetry information during search: if the depth-first search process hits a partial instantiation that is symmetrical to an instantiation which already triggered a backtrack, then it is of no use to go deeper: the solver backtracks.

The bottom line when considering symmetries is to only try to exploit them if detecting them costs less than the speedup you can get from exploiting them.

« Previous | Up ↑ | Next »